§ 5.3. Комплексные числа

Комплексными числами называются выражения

где - действительные числа, а - специальный символ; при этом для комплексных чисел введены понятии равенства и арифметические операции по следующим правилам:

1) тогда и только тогда, когда ; .

2) .

3) .

4) .

Из и следует, что

Таким образом, введенные операции сложения и умножения обладают свойствами коммутативности , ассоциативности , , дистрибутивности .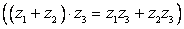

Можно еще сказать, что с комплексными числами можно оперировать в точности так же, как мы привыкли оперировать с буквенными выражениями в алгебре, но при этом операции упрощаются тем, что .

Из свойства следует, что множество комплексных чисел содержит в себе как часть множество всех действительных чисел. При этом легко видеть, что применение арифметических действий к выражениям приводит соответственно к .

Число называется сопряженным к комплексному числу . Действительное число называется модулем комплексного числа . Очевидно, что .

Если комплексное число трактовать как точку (вектор) плоскости , то равен расстоянию точки от начала координат (рис. 74).

Рис. 74

Если на плоскости ввести полярные координаты , то

. (1)

В силу этого, комплексное число можно записать в форме

, (2)

где - модуль числа , - угол (в радианах), который составляет вектор с положительным направлением оси . Этот угол называют еще аргументом комплексного числа и обозначают символом .

Очевидно, есть однозначная функция от . Вводят еще и многозначную функцию (аргумент с большой буквы)

которая дает все значения , для которых для данного удовлетворяются два равенства (1).

Число единственное, для которого не имеет смысла его аргумент, но зато его можно определить как число, модуль которого равен нулю .

(с малой буквы) называют еще аргументом в приведенной форме. Иногда бывает удобно считать аргументом в приведенной форме угол, принадлежащий к другому полуинтервалу длины , например .

Числа и называют действительной и мнимой частями и обозначают символами . Таким образом,

Если , то множество точек плоскости , удовлетворяющих равенству , есть окружность радиуса с центром в начале координат.

По определению

. (3)

Очевидно, что есть комплексная функция (принимающая комплексные значения) от действительного аргумента . Ясно, что - периодическая функция периода : .

Так как , то при непрерывном изменении на полуинтервале , точка непрерывно описывает окружность радиуса 1 с центром в точке .

Справедливы равенства

. (4)

В самом деле,

Для произвольной комплексной переменной функция определяется при помощи равенства

Отсюда в силу (3)

. (5)

На основании (2), (3) всякое комплексное число можно представить в форме

, (6)

где неотрицательное число для данного единственно, а при угол

определен с точностью до .

Выражения (2) и (6) называются соответственно тригонометрической и показательной формами комплексного числа .

Приведем примеры комплексных чисел, записанных в показательной форме (считая ):

Из равенств (3), (4) легко получаем формулу Муавра

. (7)

Справедливо также равенство

т. е. при перемножении комплексных чисел их модули перемножаются, а аргументы складываются независимо от того, в какой форме они взяты – в приведенной или нет.

Операция построения сопряженного комплексного числа обладает следующими простыми свойствами:

. (8)

В самом деле,

;

далее, так как

то

Подобное доказательство имеет место и в случае частного.

Рассмотрим задачу о вычислении корня -й степени из числа . Требуется, таким образом, найти все числа такие, что . Но тогда и, вследствие единственности представления комплексного числа в показательной форме, . Из первого равенства следует ( - арифметическое значение корня -й степени из положительного числа ). Из второго же, что .